Results
Optimization: signal detection threshold
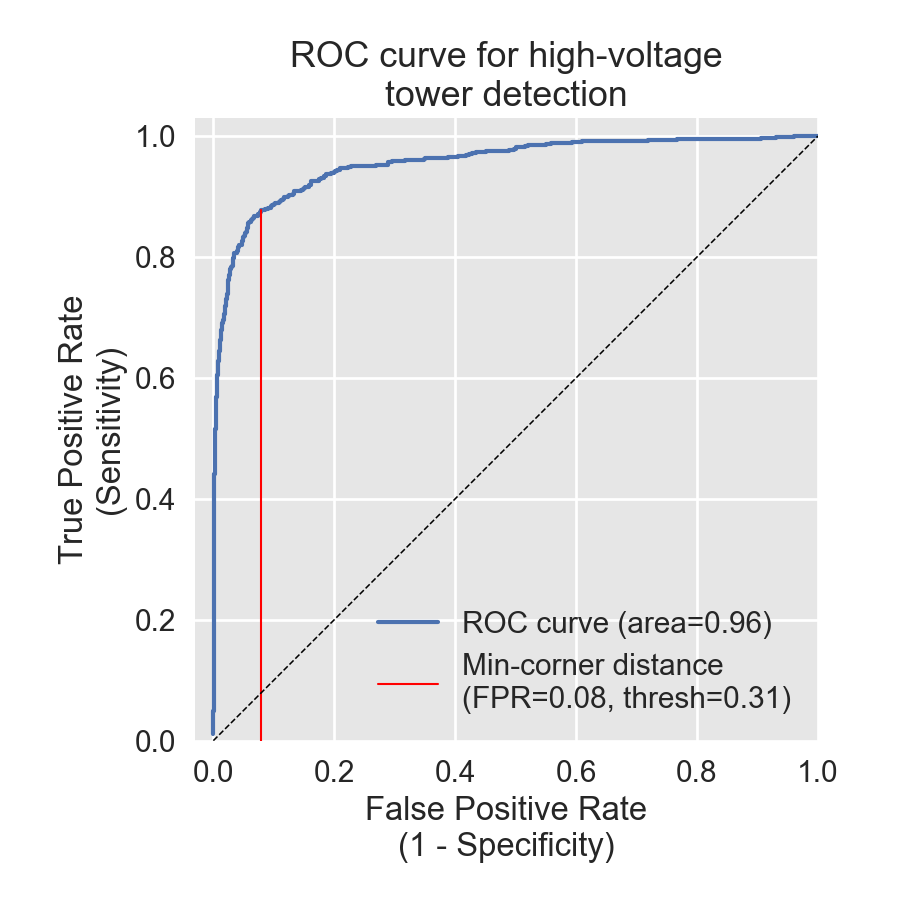
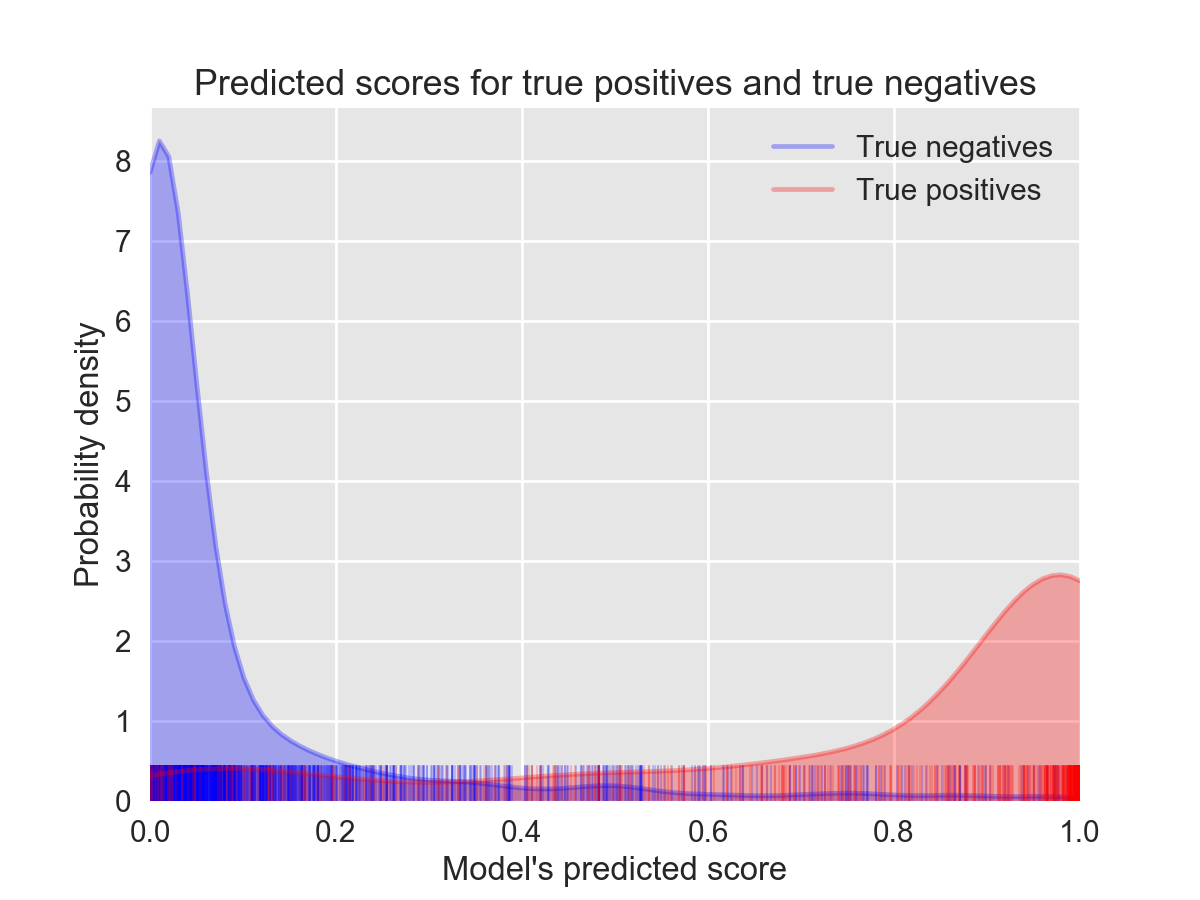
Our ML model took individual images as input and provided output for each in the form of a probability between zero and one. This probability score represents the model's confidence that a HV tower was present. Therefore, we framed this problem with a perspective borrowed from signal detection theory. This field provides theoretical guidance on how to select a threshold cutoff when deciding which images are said to contain towers and which aren’t. Here, this threshold defines which tiles should be included in the map overlay provided to the Data Team. We used ROC analysis from signal detection theory to inform this choice of threshold; an ROC curve gives insight into how our the true positive-rate (TPR) and false-positive rate (FPR) change for different choices of the threshold. The TPR gives the proportion of tiles truly containing a HV tower that were selected by the ML model. The FPR is the portion of model selections that were incorrect (i.e., probability of a false alarm). We obtained an area under the curve (AUC) of 0.96 in held out data from the three train regions with a threshold=0.31 (Figure 11). The probability score distributions for the held-out data in the training phase show good separation between true positive and true negatives (Figure 12).
Figures 11 and 12 indicated very high performance, but note that this is specific to data from the small training data set (covering about 1.05% of the combined total area of the three countries). When running this model at the country-wide scale, we noted a substantial drop in performance. Reason for this drop and potential ways to ameliorate the issue are explained in the discussion section. Briefly, we believe the problem lies with the fact that we only created training data from one small region in each country.